Thursday July 15, 2021
Environmental Awareness
Caution: Do not take what is written here as advice from an expert. I am still learning about this topic and I am not prescribing what one should do with their system. It is only a description of what I am trying to learn and the possible actions I might take.
I learned a word for something that I was trying to describe yesterday. Symlink or symbolic link. That is what the /usr/local/bin contains. So, the version of python that we find there is not the content filled directory itself but a symbolic link that points to the content filled directory. That content filled directory lives in the /usr/local/lib directory, from what I can tell.

Image by Shinichi Okada.
My plan is to keep python3.9 in the bin directory. Because its site-package is already clean, I want it to stay as my default. My previous version, 3.8, is has a site-package directory full of packages which I am considering cleaning or simply deleting that version and reinstalling it with pyenv.
I had some questions about specifics like where should I install jupyter or should I start to implement the use of pip install --user. I decided that packages such as Jupyter, venv and pip will install where they install by default in the site-package directory of the default python3 of my system which is now python3.9. From there I can create vitrualenvs and have their packages within. I am reading that –user package installation shouldn’t be used with virtual envs because they link to different locations. --user installs to its own isolated location that is not the same location as where virtual environments install to or access from.
I don’t know where pyenv will install but seeing that I install it with Homebrew. I now know this a macOS package manager so I imagine it will make system level changes like it did with python3.9. So I suppose I should start first with pyenv and then everything else after.
But one thing seems clear, that I should install pyenv and pyenv-virtualenv if I want to work on personal projects. This seems to be because it reduces the legwork of setting up each environment individually and allows for more than one project to work in the same environment, with the python version being directly linked to that environment. That environment should have all the general dependencies for that version.
Whereas, if I use pipenv then that creates a restriction that each environment must be setup individually and exclusively for each project being that there is a higher necessity for the environment to be an exact replication of the client’s environment. Where you are able to link more than one environment to a python version. This is the recommended set up for professionals working with teams and different systems.
Stats Corner
I took a break and learned something about why we use n-1 when calculating ….ehm…..sorry….estimating sample variance. Thanks to StatQuest for this explanation.
So, the sample variance formula is : ∑(x-x̄)^2 / n-1
And, the population variance is: ∑(x-μ)^2 / n
The problem is that the differences between the values of the sample data and the sample mean(x̄) is always less than the differences between the values of the population data and the population mean(μ). And when we apply this to the variance formula we increase the effect because we are squaring the differences.
If we plot all the values of the variance as y for each possible value of a mean as x for a specific set of data we get a line like this:
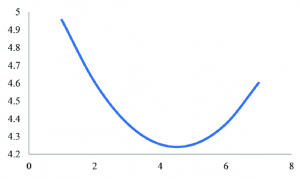
The derivative is a tangent line that intersects one point of the plotted line on a graph. When the slope of this line reaches zero, we know we have found the value of the variance at the y-value.
The sample mean always fits the sample data more tightly and thus has a lower variance when dividing by n than it would with the population mean.
Regardless, if the sample mean is higher or lower than the population mean, the issue that affects the variance is the measure of difference. That is why we also have the formula for Mean Absolute Deviation = ∑|x-x̄|^2 / n-1 which replaces the squared differences with absolute value of the differences from the average. Not only that, but is skips the need to apply the square root to the variance to give us the standard deviation, that is only apparently.
It is important to understand that estimations are exploratory and not written in stone. If we graph the squared variance with all possible values of sample or population mean (x̄, μ) for the x-values like we did before and the resulting variance for the y-values (see the plot above) statisticians were actually searching for the y-value where the slope of the derivative was zero. That process is impossible when graphing the absolute value function which creates and angle. You cannot find derivatives with and angle since a tangent must pass through one point of the line.
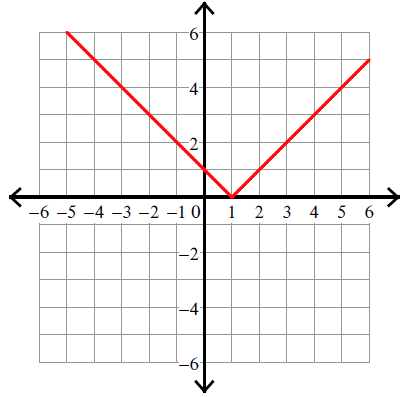
And that is why we don’t usually use the formula with the absolute value to determine variance.
I think I could explain most of this a lot better. But watch the StatQuest video for more clarity.